Differential Privacy (DP) is a means in cryptography that can improve the accuracy of data queries from statistical databases while helping to minimize the opportunity to identify specific records. DP is generally divided into: CDP (Centralized Differential Privacy), LDP (Local Differential Privacy).

First, CDP

1.1 Basic Definition

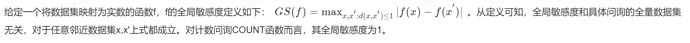
1.4 Data Clipping

The GS of the COUNT function is always 1, but the GS of the SUM function is not so straightforward, as it depends on which attribute column the SUM is applied to, such as: there is a significant difference in the application of SUM to age and income. As described in section 1.2, when we apply the Laplace perturbation mechanism, we need the bounded global sensitivity of f(x) (here SUM), but SUM is obviously not easy to achieve, so we need to clip the columns to be processed to obtain the bounded global sensitivity of f(x). Two points need to be paid special attention to:

• Perform a trade-off between the information loss caused by clipping and the noise required to satisfy differential privacy. Generally, after clipping, it is necessary to retain as much as 100% of the information.

• It is not possible to determine the clipping boundary by examining the dataset, as this may leak information and does not satisfy the definition of differential privacy.

How should we perform the clipping operation on attribute columns? Generally, there are two approaches:

• Determine the clipping boundary based on some inherent properties of the dataset. For example, human age generally ranges from 0 to 125 years.

• 采用差分隐私问询估计选择的边界是否合理。先通过数据变换把属性列映射为非负值，然后将裁剪下界置 0，逐渐增加上界，直至问询输出不变。

1.5 Vector-valued Function and Its Sensitivity

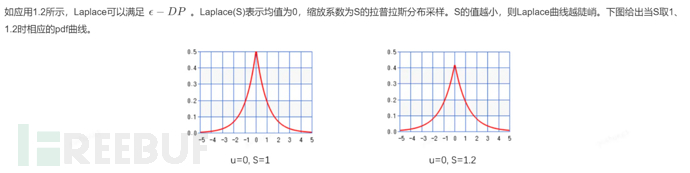
1.6 Laplace Mechanism

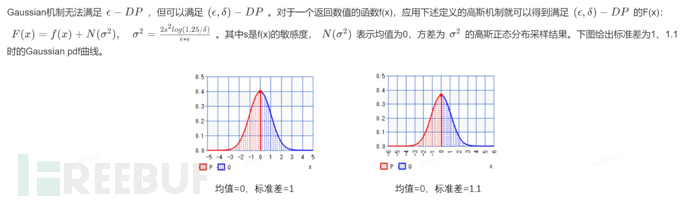
1.7 Gaussian Mechanism

1.8 Laplace vs Gaussian

The vector-valued Laplace mechanism requires the use of L1 sensitivity, while the vector-valued Gaussian mechanism can use both L1 and L2 sensitivity. In scenarios where the L2 sensitivity is much lower than the L1 sensitivity, the noise added by the Gaussian mechanism is much smaller. The publication rules for vector-valued Laplace and Gaussian are as follows:

1.9 Exponential MechanismThe responses of the aforementioned Laplace and Gaussian mechanisms are all numeric, and noise can be directly added to the numeric result of the response. If we want to select the best result from a set of alternative responses while ensuring that the response process satisfies differential privacy, what should we do?One feasible method is to use the exponential mechanism.

Firstly, define a set of alternative responses; then, define the scoring function, which outputs the score of each response in the alternative set; the response with the highest score is the maximum response. The exponential mechanism achieves differential privacy protection by returning the response with the highest score approximately.

You can see that, compared with the Laplace mechanism, the difference of the exponential mechanism is that it always outputs an element from the set R.

options =adult['Marital Status'].如下我们给出有限集合的指数机制代码样例()1000score(unique,data)defreturnunique.value_counts()[data]# 根 据 分 数 计 算 每 个 回 复 的 输 出 概 率option1000exponential(u,R,:,*,exp)defsensitivity =[:(u,r)forr inR]x probabilities =[np.# 计 算R中 每 个 回 复 的 分 数(exp 2score # 根 据 分 数 计 算 每 个 回 复 的 输 出 概 率(epsilon2*))forscore insensitivity]scores  probabilities =probabilities # 根 据 分 数 计 算 每 个 回 复 的 输 出 概 率np./.norm(probabilities,ord=1)# 对 概 率 进 行 归 一 化 处 理 ， 使 概 率 和 等 于1returnnp.random.choice(R,1,p=probabilities)[0]# 根 据 概 率 分 布 选 择 回 复 结 果exponential(adult['Marital Status'],options,score,1,1)# 输出 'Married-civ-spouse'r =[exponential(adult['Marital Status'],options,score,1,1)fori inrange(200)]pd.Series(r).value_counts()# output: Married-civ-spouse 185     Never-married 15

Report the maximum noise value

When R is a finite set, the basic idea of the exponential mechanism is the process of selecting elements from the set, which satisfies differential privacy. This idea can be implemented naively using the Laplace mechanism:

def report_noisy_max(x, R, u, sensitivity, epsilon):
    scores = [u(x, r) for r in R]     # Calculate the score of each reply in R
    noisy_scores = [laplace_mech(score, sensitivity, epsilon) for score in scores]    # Add noise to each score
    max_idx = np.argmax(noisy_scores)   # Find the reply index number corresponding to the maximum score
    return R[max_idx]   # Return the reply corresponding to this index number
report_noisy_max(adult['Marital Status'], options, score, 1, 1)   # output: 'Married-civ-spouse'

r = [report_noisy_max(adult['Marital Status'], options, score, 1, 1) for i in range(200)]
pd.Series(r).value_counts()  # output: Married-civ-spouse 196    Never-married 4

1.10 Composability and post-processing

When publishing results protected by multiple differential privacy mechanisms on the same input data multiple times,Serial compositionalityIt provides the total privacy consumption. The specific content is as follows:

Second, LDP

2.1 Basic Definition of LDP

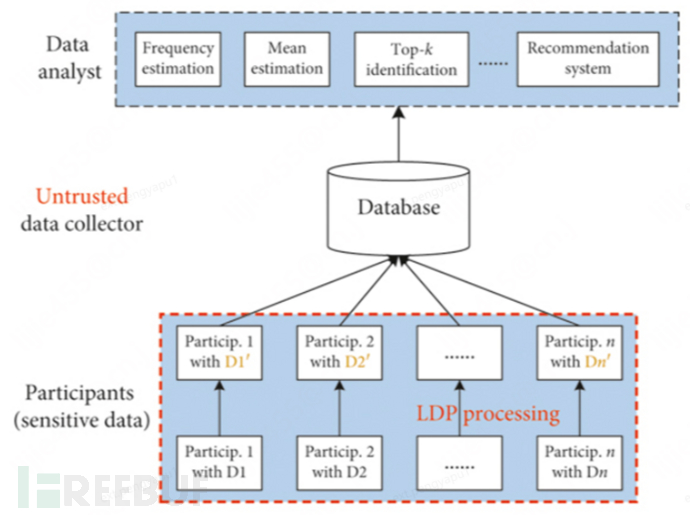
Privacy protection effect: other roles (client or central server) cannot distinguish different samples in client A.The corresponding algorithm architecture is as follows:

2.2 Classic LDP Algorithm

Based on random response

•Binary discrete variables: W-RR, see example 2.3

•Multivalued discrete variables (binary encoding): RAPPOR, SHist

•Multivalued discrete variables (improved probability distribution): K-RR, GRR, ORR

•Processing multi-dimensional numerical variables: pMeanEst, Harmony-mean (sampling)

Interference mechanism based on information theory

•Compression

•Distortion

2.3 Example of LDP - Random Response

There are n users, assuming the true proportion of patients with disease X is Π, we hope to conduct a statistical analysis of this proportion. Therefore, we initiate a sensitive question: 'Are you a patient with disease X?' Each user's answer is yes or no. Considering privacy, users may not give the correct answer [5].

We can add some data perturbation to each user's answer. For example: the probability of a user answering correctly is p, and the probability of answering incorrectly is (1-p). In this way, we will not be able to accurately know the true answer of each user, which is equivalent to protecting user privacy. According to this rule, we count the proportion of users who answer yes and no.

The application of DP in the field of machine learning, and the principle of realizing LDP based on Gaussian mechanism will be shared in the next episode.

Instance verification

A total of n = 50 people (known), including 10 positives (unknown), and 40 negatives (unknown). Each person reports the truth with a probability of p = 0.8 (known). The statistical results are as follows:

•Positive statistical value n1 = 10*0.8 + 40*0.2 = 16

•Negative statistical value = 40*0.8 + 10*0.2 = 34

The corrected positive value = 50*(-1/3) + 160/6 = 10

Reference materials

1.Balle B, Wang Y X. Improving the gaussian mechanism for differential privacy: Analytical calibration and optimal denoising[C]//International Conference on Machine Learning. PMLR, 2018: 394-403.

2. https://programming-dp.com/

3.Cynthia Dwork, Aaron Roth, and others. The algorithmic foundations of differential privacy. Foundations and Trends® in Theoretical Computer Science, 9(3–4):211–407, 2014.

4.Xiong X, Liu S, Li D, et al. A comprehensive survey on local differential privacy[J]. Security and Communication Networks, 2020, 2020: 1-29.

5. Example of LDP Random Response Technology: https://zhuanlan.zhihu.com/p/472032115

Author: JD Technology, Li Jie

Content Source: JD Cloud Developer Community