0x1. Introduction

You may look down upon this, but if pq is very close, yafu can be used to solve it directly, and there is no need for us to worry about solving it. What is the significance of writing this article? That's right, I also thought so before, but in fact, it is not. The facts have proven that some things still need to understand some principles to belong to you, otherwise, some problems slightly changed and you will not know how to solve them.

So today, I come to record this issue carefully.

0x2. Main Text

1. Problem expression and yafu decomposition

First, what does it mean that the values of pq are close to each other, in the problem, it usually refers to such a meaning:

from Crypto.Util.number import getPrime
import gmpy2
p = getPrime(512)
q = gmpy2.next_prime(p)
n=p*q
print('n =', n)

Let's directly generate an instance to demonstrate:

The value of n is 149508848441616715934297319023960757580837139746636486446093766820602595577720613880522359931376776640771560399865570788752926866918099448386204160338951577084579042581094657939545555751085950319193925075988080113525569558968885659546782419751524189916167947489803707492932640059831396220643698853028753007377

Well, this is very common, we usually use yafu to directly decompose two p and q:

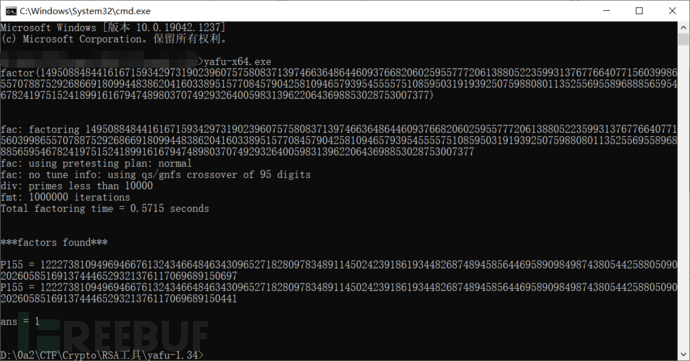
Then the subsequent operations are very simple, the problem is, if we ourselves use the script to calculate how to calculate it?

2. Python script decomposition

Think about this problem carefully, in fact, there are many methods, let's list them one by one.

2.1. Simple idea

We take the square root of it directly, and the integer value after taking the square root must be between the two numbers, because they are throughnext_primeSince they are connected, we can be sure that there are no prime numbers between them, so we can directly use anext_primeOnce we get the larger prime number p, we also know the other prime number q.

The script is as follows:

import gmpy2
The value of n is 149508848441616715934297319023960757580837139746636486446093766820602595577720613880522359931376776640771560399865570788752926866918099448386204160338951577084579042581094657939545555751085950319193925075988080113525569558968885659546782419751524189916167947489803707492932640059831396220643698853028753007377
tmp = gmpy2.iroot(n, 2)[0]
p = gmpy2.next_prime(tmp)
q = n // p
print("p=",p)
print("q=",q)

The reason is very simple, let's run and see:

It can be found that the answer is the same as that calculated by yafu before.

2.2. Another method

This method is basically the same as the previous one, and it also uses the square root of n to obtain the result. So, what is the difference? First, it can obtain the two solutions p and q at one time, and it also has other advantages. Let's look at the method first:

import gmpy2

def factor(n):
a = gmpy2.iroot(n, 2)[0]
while True:
a += 1
b2=a*a-n

if gmpy2.is_square(b2):
 b2 = gmpy2.mpz(b2)
 b, xflag = gmpy2.iroot(b2, 2)
 assert xflag
 return (a-b, a+b)

The value of n is 149508848441616715934297319023960757580837139746636486446093766820602595577720613880522359931376776640771560399865570788752926866918099448386204160338951577084579042581094657939545555751085950319193925075988080113525569558968885659546782419751524189916167947489803707492932640059831396220643698853028753007377
p,q=factor(n)
print("p=",p)
print("q=",q)

Let's first look at the running results:

The answer is the same as before, but perhaps you still have some doubts. What is the principle of this script? Why is it written like this? What are the benefits?

I will explain one by one.

You can see that this script is very different from the previous script, so what principle does it use?

If you look carefully, you can see that the returned p and q are actually two temporary parameters in the decomposition functiona-ba+b

a is straightforward, a is the integer square root of n, which is easy to understand, but what is the generation of b? There is also a mysterious formula:b2=a*a-n

First, list a formula:n=p*qp=a-bq=a+bn=(a-b)*(a+b)n=a*a-b*bAnd b2 is not the square of b, so there isn=a*a-b2b2=a*a-nthere is no problem.

So we find that this code is actuallyUnder the premise of traversing a, find out all feasible bn=(a-b)*(a+b)This formula, thus obtaining p and q.

And the value of a is from small to large throughout the brute-force process, and correspondingly, the value of b is also from small to large, becauseb*b=a*a-nWith the increase of a, b will also increase, and correspondingly, the two solutions:a-ba+bb=0a*aThis is equivalent to the 'midpoint' of solving between 0 and n, so we can understand thatThis script starts from the 'midpoint' of n's square root and gradually scans both sides until it gets the solution ora-b==0So in principle, it can brute-force all solutions

Alright, we understand the principle, so we know that this script is actually a brute-force script that tries every possibility until it gets the solution, soThis script can only be used when the initial value and the solution are close.If you start brute-forcing from 0, it would take an eternity.

So why do it this way?

You can find that this script is a brute-force script, but it is not as simple and clear as the first script. So, what is its use?

The advantage is that this script is a brute-force script, so it can brute-force all possible solutions. Naturally, this example doesn't show anything because there is only one solution, and when there is only one solution, either of the above two scripts can get the correct solution.

At the same time, it will not be affectednext_primelimit, if the solution is not a prime number, it will also find the solution.

This is very useful in some slightly modified questions.

Let us illustrate this solving method with an example.

3. Variant of the problem

3.1. When two similar factors are present

The reference here is part of a recent competition, the Green City Cup competition: 【Green City Cup】RSA2-PLUS

Partial source code is as follows:

from Crypto.Util.number import *
import gmpy2
from flag import flag
assert flag[:5]==b'flag{'

m1 = bytes_to_long(flag[:20])
p  = getPrime(512)
p1 = gmpy2.next_prime(p)
q  = getPrime(512)
q1 = gmpy2.next_prime(q)
n1 = p*q*p1*q1
print('n1 =',n1)
e = 0x10001
c1 = pow(m1,e,n1)
print('c1 =',c1)

The value of n1 is 6348779979606280884589422188738902470575876294643492831465947360363568026280963989291591157710389629216109615274754718329987990551836115660879103234129921943824061416396264358110216047994331119920503431491509529604742468032906950984256964560405062345280120526771439940278606226153077959057882262745273394986607004406770035459301695806378598890589432538916219821477777021460189140081521779103226953544426441823244765828342973086422949017937701261348963541035128661464068769033772390320426795044617751909787914185985911277628404632533530390761257251552073493697518547350246993679844132297414094727147161169548160586911
The hexadecimal number #c1 is 6201882078995455673376327652982610102807874783073703018551044780440620679217833227711395689114659144506630609087600915116940111002026241056808189658969089532597757995423694966667948250438579639890580690392400661711864264184444018345499567505424672090632235109624193289954785503512742400960515331371813467034511130432319427185134018830006918682733848618201088649690422818940385123599468595766345668931882249779415788129316594083269412221804774856038796248038700275509397599351533280014908894068141056694660319816046357462684688942519849441237878018480036145051967731081582598773076490918572392784684372694103015244826

It looks similar to the above question, but the difference is that n is composed of four prime factors, of which two are paired and approximately equal, of course, we cannot use the first script approach at this time, because no matter how many roots, it is unlikelynext_primeExactly equal to the true p and q, at this time we can also try to decompose with yafu directly:

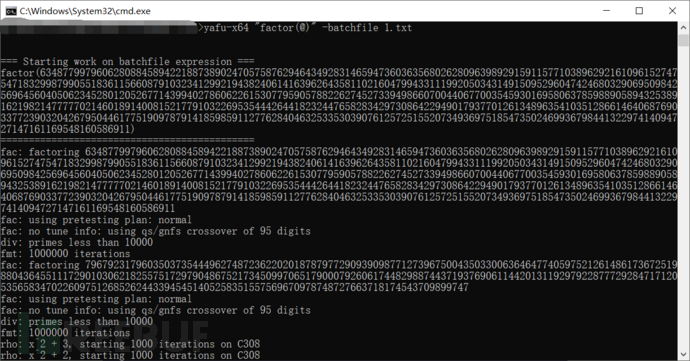
If we keep calculating, it will never end, and we can find a solution in the process of termination of calculation, but this solution is actually not a prime number:

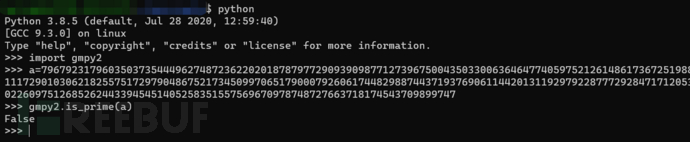
Therefore, the solution we calculate is not one of the four factors of n, but the product of two of them, and the value obtained by dividing n by this solution is the product of the other two factors, which is not helpful to us in calculating the Euler's totient phi.

So how can we get the complete values of the four factors?

Let's take a look at the construction of these four factors first:

p  = getPrime(512)
p1 = gmpy2.next_prime(p)
q  = getPrime(512)
q1 = gmpy2.next_prime(q)

That is to say, p and p1 are close, q and q1 are close, we do not know who and whose product yafu has calculated at this time, perhapsp*qOrp1*q1Perhapsp*q1Orq*p1No matter what, we find a very interesting feature, that is, on both sides of the 'middle value' of the square root of n1, there are these two very close solutions:(p*q)*(p1*q1), (p*q1)*(q*p1)Then if we use the second method of the above script, we can break out these two non-prime solutions in a short time, because we know that it actually starts from the 'middle' and explodes to both sides, once we have both sets of solutions, finding their common factors can get the value of q or p, and thus get the values of all four factors.

It should be noted that the decomposition of n is not only these two sets of solutions, but also includes a total of 8 sets of solutions, including(p)*(p1*q*q1), (p*p1)*(q*q1)Such a solution, but we know that the two groups of solutions are very close to the starting point of our brute force, which has caused our exploitation.

With this idea, we can write the following code:

import gmpy2

def fermat_factorization(n):
factor_list = []
a = gmpy2.iroot(n,2)[0]
while True:
a += 1
b2 = a * a - n

if gmpy2.is_square(b2):
 b2 = gmpy2.mpz(b2)
 b,xflag = gmpy2.iroot(b2,2)
 assert xflag
 factor_list.append([a + b, a - b])
 if len(factor_list) == 2:
  break
return factor_list

n1 = 6348779979606280884589422188738902470575876294643492831465947360363568026280963989291591157710389629216109615274754718329987990551836115660879103234129921943824061416396264358110216047994331119920503431491509529604742468032906950984256964560405062345280120526771439940278606226153077959057882262745273394986607004406770035459301695806378598890589432538916219821477777021460189140081521779103226953544426441823244765828342973086422949017937701261348963541035128661464068769033772390320426795044617751909787914185985911277628404632533530390761257251552073493697518547350246993679844132297414094727147161169548160586911
factor_list = fermat_factorization(n1)
X1, Y1 = factor_list[0]
X2, Y2 = factor_list[1]
assert X1 * Y1 == n1
assert X2 * Y2 == n1
p = gmpy2.gcd(X1, X2)
q = X1 // p
p1 = gmpy2.gcd(Y1, Y2)
q1 = Y1 // p1
print('p=', p)
print('q=', q)
print('p1=', p1)
print('q1=', q1)

Execution, successfully obtained four prime numbers:

The numerical order may be different from the original, but it does not matter, as long as we get the result.

The next step is the normal RSA decryption process, and it will not be elaborated here.